Fue ideado por Jacob Ziv y Abraham Lempel, y publicado en el IEEE Transactions on Information Theory, vol. IT-23, No 3 de Mayo de 1977, si bien ya hab�a sido presentado anteriormente en el IEEE International Symposium on Information Theory celebrado en Ronneby, Suecia, en Junio de 1976.
Desde entonces recibe el nombre de compresi�n Lempel-Ziv o, para abreviar, LZ.
Existe una variante de LZ, denominada LZW (Lempel-Ziv-Welch), que se ha hecho muy famosa por ser la que se utiliza para comprimir en el formato de im�genes GIF. Se trata de una modificaci�n de LZ que, a costa de un menor ratio de compresi�n, ofrece mejoras en cuanto a velocidad y uso de memoria, lo que hizo que se usara en los modems que soportan el protocolo V42bis. Es tambi�n el algoritmo empleado en el programa compress. Sin embargo, a pesar de su atractivo, no lo trataremos aqu� porque, desgraciadamente, se trata de un algoritmo sujeto a patentes. Pese a que la informaci�n sobre su funcionamiento se encuentra accesible l�bremente ("A Technique for High-Performance Data Compression'', Terry A. Welch, IEEE Computer, Junio 1984, p�ginas 8-19), su funcionamiento en cambio no lo es. Contrariamente a lo que se podr�a pensar, la patente no es de Terry Welch, que durante 7 a�os, y hasta que en 1983 se march� a DEC, estuvo trabajando en el Sperry Research Center de Sudbury, Massachusetts. Desde el principio fue Sperry el propietario de la patente, aunque nunca trat� de sacarle partido. Al menos hasta que en 1986 se uni� a Burroughs para formar Unisys. Fue entonces cuando empezaron a utilizarla contra los fabricantes de modems. Actualmente la patente pertenece a Unisys, que legalmente puede cobrar por su uso, como ya hizo con Compuserve, con la que lleg� a un acuerdo para crear una licencia para productores de software sobre el formato GIF, que antes era libre. No obstante lo dicho, Unisys al final decidi� no cobrar derechos de patentes por c�digo libre que se hubiera publicado con anterioridad a la decisi�n de hacer efectiva la patente, y por ello hay una librer�a -giflib- que se puede usar para c�digo libre sin pagar patentes; la librer�a est� ahora mantenida por Eric S. Raymond: http://www.ccil.org/ esr/giflib.
La idea en que se basa LZ resulta simple, visto todo lo que le hemos pedido al algoritmo en la secci�n anterior: b�sicamente busca secuencias repetidas dentro de los datos, y cada vez que encuentra una de ellas la reemplaza por un puntero a la zona en la que comienza la primera secuencia, m�s la longitud que se debe tomar a partir de esa posici�n. En caso de que no haya repeticiones, se emite la secuencia como un literal.
Lo m�s importante, y lo que conforma el n�cleo de la idea, es identificar lo que Lempel-Ziv llaman extensi�n reproducible de una cadena dentro de otra y que difiere un tanto de lo que coloquialmente llamamos "repeticiones''.
Ve�moslo con el mismo ejemplo del art�culo original de los autores, pero desde un punto de vista m�s descriptivo y menos matem�tico para facilitar un poco su lectura: supongamos que tenemos la secuencia S=00101011. Pong�moslo tabulado, de forma que podamos hacer referencia a cada elemento de la secuencia fij�ndonos en el orden en el que aparece dentro de esta. La primero fila de la figura 1 indica la posici�n dentro del buffer y la segunda su contenido. Consideraremos la posici�n m�s a la izquierda como posici�n 1.

Supongamos tambi�n que los tres primeros elementos, 001, ya han sido codificados; en este momento nos da igual que hayan sido comprimidos o tomados como literales. Posteriormente nos ocuparemos de ese aspecto, pero ahora tenemos que codificar lo que sigue: 01011. Llamaremos a la secuencia ya codificada secuencia 1 y a la que est� siendo codificada ahora secuencia 2.
Si a una persona normal le pedimos que encuentre en 01011 una secuencia que est� repetida a partir de lo que ya hemos codificado (001), nos dir� que los dos primeros elementos de la secuncia a codificar (posiciones 4 y 5 dentro del buffer) son iguales a los dos �ltimos de 001 (posiciones 2 y 3), y que ah� hay una repetici�n. Y tendr� raz�n, pero la genialidad de LZ est� en darse cuenta de que se puede ir m�s all� y utilizar la propia secuencia a codificar como lugar donde seguir buscando repeticiones. �Eso a pesar de que a�n no la hemos codificado!
Ve�moslo: la secuencia 2 empieza por 0101 (posiciones 4 a 7). Si empezamos a mirar en lo que ya hemos codificado, la secuencia 1, tenemos que finaliza en 01, pero si seguimos entrando en la secuencia 2 ahora veremos que empieza por 01. Si juntamos el final de la secuencia 1 con el principio de la secuencia 2, tenemos 0101, que es igual al comienzo de la secuencia a codificar o secuencia 2. Es decir: los elementos 4, 5, 6 y 7 de la secuencia total son una "repetici�n'' de los elementos 2, 3, 4 y 5. Por tanto se codificar�n como un puntero a la posici�n n�mero 2 m�s una longitud de 4. Luego veremos en un ejemplo c�mo esto, aunque parezca imposible, funciona a la hora de decodificar.
La codificaci�n se lleva a cabo introduciendo los datos dentro de un buffer de una longitud prefijada, n, dentro del cual se van buscando subcadenas ya repetidas haciendo uso del m�todo que acabamos de explicar. En gzip, la longitud m�xima de esas subcadenas, Ls, es de 258 bytes. Si una cadena no ocurri� dentro de los 32 Kbytes anteriores, se emite literalmente.
Un ejemplo ayudar� a ver c�mo se llevan a cabo la compresi�n y la descompresi�n. Utilizaremos una simplificaci�n de uno propuesto por los creadores del algoritmo. Supongamos que queremos codificar la secuencia S=001010210210212021021200... Por razones did�cticas (aunque no pr�cticas) usaremos un buffer de longitud n=18 y una longitud m�xima de cadena Ls de 9. Inicialmente se llenan las n-Ls posiciones del buffer con ceros, y las Ls restantes con los primeros datos de la secuncia, con lo que el buffer en la posici�n inicial quedar�a como se ve en la figura 2.

La extensi�n reproducible de Ls, empezando a buscar en la parte ya "codificada" (las n-Ls primeras posiciones del buffer), aparece en gris. La primera subcadena a codificar se formar� a partir de esa extensi�n reproducible, 00, seguida del siguiente elemento que ya no est� repetido 1, luego S1=001. La palabra c�digo que representa a esa subcadena ser�, por convenio y en ese orden, el puntero al comienzo de la repetici�n menos 1, seguido de la longitud de la repetici�n, seguido del elemento final, que no entraba en la repetici�n. Es decir, para este caso: C1=021.
Puesto que S1 ten�a longitud 3, todo el contenido del buffer es despplazado hacia la izquierda 3 posiciones. En esta situaci�n 2 seguiremos, como siempre, a partir de la posici�n 10, buscando la extensi�n reproducible de 0102... La encontramos en la figura 3.

Aqu�, la extensi�n peri�dica de los elementos a partir de la posici�n 10 se haya en la posici�n 8. Empezando tanto por 8 como por 10 encontramos la secuencia 010, as� que S2 es la parte que se repite del comienzo de Ls, 010 (posiciones 10 a 12), m�s el siguiente elemento, 2, que ya no se repite (posici�n 13). Luego S2=0102, que se codifica cmo C2=732. Desplazamos 4 posiciones a la izquierda, que es lo que mide S2, y la "repetici�n'' de la secuencia Ls se encuentra en la zona marcada en la figura 4.

En ella se observa con claridad que, dado que Ls empieza por 10, hab�a una repetici�n en las posiciones 5 y 6, que tambi�n son 10, que sin embargo no hemos marcado en negrita dentro de la figura. Esto es debido a que la secuencia formada por las posiciones 5 y 6, si bien representa una repetici�n de lo que aparece en Ls, no se trata de su extensi�n peri�dica ya que tiene longitud 2, mientras que la coloreada en la figura tiene longitud mayor: 7. Por ello S3=10210212 y C3=672. Por �ltimo, tras desplazar las 8 posiciones que ocupa S3, se obtiene S4=021021200 y C4=280 (figura 5).

Comprobemos que la secuencia comprimida C=821732672280 puede decodificarse un�vocamente dando como resultado la secuancia original S=001010210210212021021200. Es importante darse cuenta de que, si bien la longitud de las subcadenas no es fija (aunque s� limitada), la de las palabras c�digo s� lo es: en este caso, 3 caracteres. Esto permite separar a partir de C palabra c�digo de palabra c�digo de forma simple. Incluso dentro de una misma palabra c�digo, los tama�os asignados a una u otra funci�n (posici�n a partir de la que empieza una repetici�n, longitud de esta y elemento siguiente a ella), son tambin fijos, y f�cilmente separables,
La longitud de cada uno de estos campos, y de la palabra c�digo como suma de todos ellos, est� directamente relacionada con el tama�o del buffer, n, y con el de la m�xima subcadena, Ls. M�s detalles se pueden encontrar en el art�culo de Lempel-Ziv.
Para descomprimir se emplea un buffer de longitud n-Ls donde se van guardando los s�mbolos descodificados. Inicialmente el buffer se pone todo a 0.
Seguidamente se van leyendo palabras c�digo, lo cual puede hacerse sin especiales cuidados al tener todas la misma longitud. Tambi�n en este caso ilustraremos la descompresi�n paso por paso. El primero se ilustra en la figura 6.
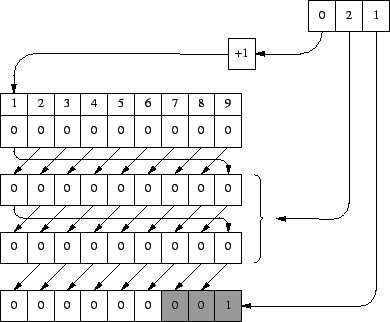
La primera palabra que se lee es '021'. El '0' sirve de puntero en el buffer, y lo llamaremos "p''. Se debe leer el car�cter que est� en la posici�n p+1, luego se lee el de la posici�n 1. Como inicialmente el buffer estaba puesto a 0, no sorprende que lo que encontremos en la posici�n 1 sea un '0'. Tal y como est� el buffer, se desplazan todos sus elementos una posici�n hacia la izquierda, y en el hueco que queda a la derecha se introduce el car�cter le�do con anterioridad en esa posici�n 1. El segundo car�cter de la palabra c�digo es un '2'. Ello indica que la operaci�n anterior de leer y desplazar se debe hacer dos veces, por lo que la repetimos: nuevamente se lee la posici�n 1. Aunque la posici�n es la misma, el dato le�do no tiene por qu� serlo, ya que el buffer se desplaz� hacia la izquierda. En este caso volvemos a tener un '0', y el buffer tiene el mismo aspecto que antes. Al segundo elemento de las palabras c�digo lo llamaremos a partir de ahora "n''. Puesto que ya hemos hecho dos veces la operaci�n, tantas como indicaba el n de la palabra c�digo que estamos decodificando, ahora se desplaza una vez m�s a la izquierda, y en el hueco que ha aparecido se introduce el tercer car�cter de la palabra c�digo (a partir de ahora "c''), sin modificar: el '1'.
Al final de todas las figuras se resalta en negrita la parte del buffer que corresponde a la descodificaci�n de la palabra c�digo. Evidentemente, este tramo se encuentra siempre al final del buffer, y su longitud es bien simple de calcular: n+1.
La siguiente palabra a decodificar es 732. Como antes, y esta vez por 3 veces, se guarda el car�cter de la posici�n 7+1 y se coloca a la derecha del buffer tras desplazarlo. El �ltimo car�cter que se introduce por la derecha nos viene dado en la palabra c�digo: ahora es un '2' (figura 7).
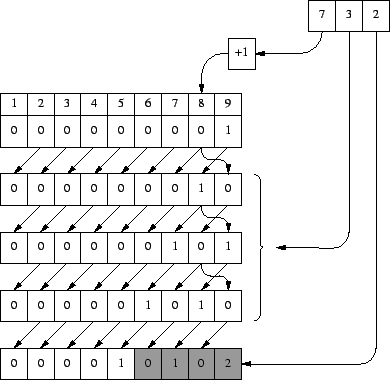
El proceso con las dos palabras c�digo restantes es exactamente igual, y no requieren mayor explicaci�n. No obstante, se ofrecen las figuras correspondientes para que el lector interesado pueda seguir el proceso hasta el final (figuras 8 y 9).
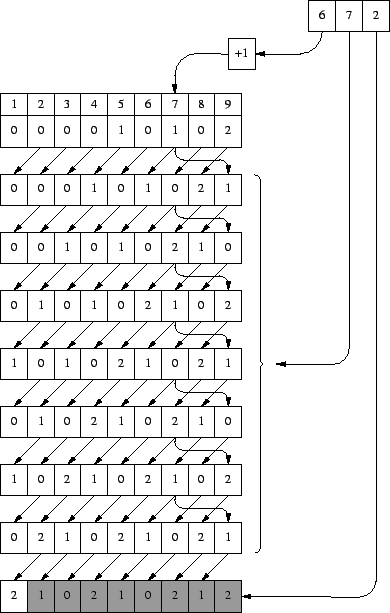
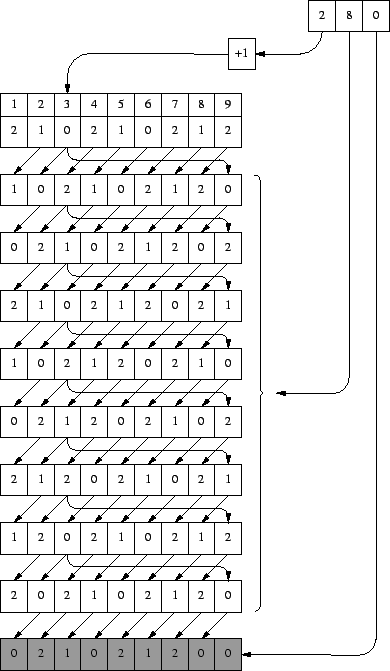
Extrayendo los tramos en negrita del final de cada paso, obtenemos 001, 0102, 10210212 y 021021200, que juntos vuelven a conformar la secuencia original S.