Los algoritmos de b�squeda son aquellos que se centran en buscar un cierto elemento dentro de un vector y, quiz�, devolver la posici�n en la que se encuentra dicho elemento. Vamos a estudiar dos algoritmos: el algoritmo b�sico de b�squeda (b�squeda secuencial), y el algoritmo de b�squeda dicot�mica. Este �ltimo es m�s r�pido que el primero, pero como contrapartida tiene que s�lo funcionar� cuando el vector en el que se busca est� ordenado. Si el vector no est� ordenado, no tiene ning�n sentido hacer una b�squeda dicot�mica.
 �Algoritmo de b�squeda secuencial
�Algoritmo de b�squeda secuencial
Es muy sencillo: se trata de recorrer el vector, elemento por elemento, preguntando si el elemento que visitamos es igual al que estamos buscando, y terminando de buscar cuando lo encontremos. El algoritmo quedar�a como sigue (nuevamente, suponemos que tratamos con un vector de enteros):
VARIABLES
encontrado: Logico;
v: Vector[1..N] de Entero;
i, elemBuscado: Entero:
FIN VARIABLES
Leer_del_teclado(elemBuscado);
encontrado = Falso;
i = 1;
mientras NO(encontrado) Y (i < N) hacer
si v[i] = elemBuscado entonces
encontrado = Verdadero;
fin si
i = i + 1;
fin mientras
Es evidente que si al terminar de recorrer el vector, tenemos que encontrado=Falso, quiere decir que no se ha encontrado el elemento dentro del vector.
 �Algoritmo de b�squeda dicot�mica
�Algoritmo de b�squeda dicot�mica
Como ya hemos dicho, este algoritmo asume que estamos trabajando con un vector ordenado. Esta asunci�n no es a la ligera, y no debemos olvidarla, como comprobaremos a continuaci�n.
La idea es empezar a buscar el elemento objetivo por la mitad del vector, es decir, miraremos si el elemento que est� en el centro del vector coincide con el elemento buscado. Si coincide, ya hemos terminado. Si no coincide, entonces miramos qu� sucede: si el elemento buscado es menor que el elemento que est� en el centro del vector, entonces s�lo buscaremos en el subvector izquierdo; si el elemento buscado es mayor que el que est� en el centro del vector, entonces s�lo buscaremos en el subvector derecho. Se entiende por subvector izquierdo el vector formado por los elementos [1..centro - 1] y por subvector derecho el vector formado por los elementos [centro + 1..N].
Dentro del subvector adecuado, repetimos el proceso: comparamos con el elemento central. Si es igual, hemos terminado, si es menor, buscamos en el subvector izquierdo, si es mayor, buscamos en el subvector derecho.
La manera de colocarnos en el subvector adecuado es por medio de tres variables auxiliares, que llamaremos izq, der y medio. En la variable izq almacenaremos la posici�n del vector que se corresponder� con el extremo izquierdo del subvector, en la variable der almacenaremos la posici�n del vector que se corresponder� con el extremos derecho del subvector, y en la variable medio almacenaremos la posici�n central del subvector.
Por ejemplo, si tenemos el vector [1, 2, 3, 4, 5], empieza siendo izq = 1, der = 5 y medio = 3. Ahora bien, el subvector izquierdo corresponder�a a izq = 1, der = 2 (= medio - 1), mientras que el subvector derecho corresponder�a a izq = 4 (= medio + 1), der = 5.
Es decir, si nos toca movernos al subvector izquierdo, ajustaremos el valor de der como der = medio - 1 dejando izq como est�, mientras que si nos toca movernos al subvector derecho, ajustaremos el valor de izq como izq = medio + 1, dejando der como est�. En ambos casos hay que recalcular medio = (izq + der)/2, ya que al movernos a cualquiera de los dos subvectores, la posici�n central cambia.
Vamos a estudiarlo con detenimiento en el siguiente ejemplo. Buscamos si el valor 12 est� en el siguiente vector:
v = [1, 2, 3, 4, 12, 13, 14]
El vector tiene N = 7 elementos, izq = 1, der = 7, medio = (izq + der) / 2 = (1+7)/2 = 4. As� que empezamos viendo si v[medio] = 12. Pero v[4] = 4, que no es 12. Ahora bien, �12 < 4? No, entonces no buscamos en el subvector izquierdo (que ser�a [1, 2, 3]). Si 12 <> 4 y no es 12 < 4, tiene que ser 12 > 4, as� que buscamos en el subvector derecho: [12, 13, 14]. Esto requiere que ajustemos los valores de izq, der y medio.
Como nos hemos movido al subvector derecho, izq = medio + 1 = 5, der = 7, y ahora medio = (izq + der)/2 = (5+7)/2 = 6 (observamos que la posici�n 6 del vector se corresponde con el centro del subvector [12, 13, 14]). As� que vemos si v[6] = 12. Pero v[6] = 13, que no es 12. �12 < 13? S�, pues entonces buscamos en el subvector izquierdo, que es [12].
Tenemos que ajustar de nuevo los valores de izq, der y medio. Como nos hemos movido al subvector izquierdo, izq se queda como est� (izq = 5), der = medio - 1 = 6-1 = 5, medio = (izq + der)/2 = (5+5)/2 = 5. As� que vemos si v[5] = 12. Efectivamente, v[5] = 12, que es el valor buscado.
Gr�ficamente (para intentar aclarar un poco m�s):
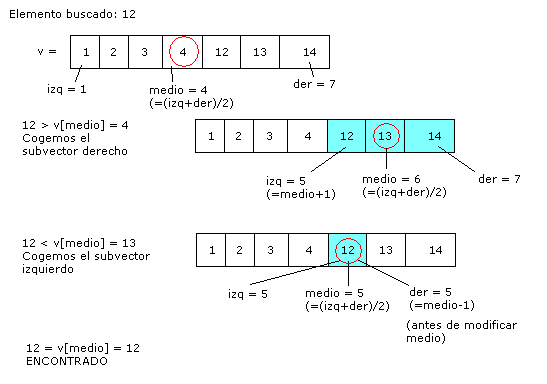
Ahora bien, �c�mo sabemos si un elemento no est� dentro del vector utilizando este algoritmo? Lo sabremos en el momento en que izq > der. Cuando se crucen los valores de izq y der es porque no se ha encontrado el elemento. Vamos a ver c�mo ser�a el algoritmo:
VARIABLES
v: Vector[1..N] de Entero;
encontrado: Logico;
izq, der, medio, elemBuscado: Entero;
FIN VARIABLES
Leer_del_teclado(elemBuscado);
encontrado = Falso;
izq = 1;
der = n;
mientras (izq < der) Y NO(encontrado) hacer
medio = (izq + der) / 2;
si v[medio] = elemBuscado entonces
encontrado = Verdadero;
sino
si v[medio] < elemBuscado entonces
izq = medio + 1;
sino (* v[medio] > elemBuscado *)
der = medio - 1;
fin si
fin si
fin mientras