�Qu� es una funci�n? Matem�ticamente, una funci�n no es m�s que una aplicaci�n, esto es, una REGLA o CRITERIO para obtener un cierto resultado a partir de unos valores ya existentes. Este concepto se ha trasladado as� al campo de la inform�tica, aunque conviene matizar un poco m�s la idea.
La idea de funci�n es la de una "caja negra" en la que nosotros metemos datos, dentro de esa "caja" pasa *algo*, y entonces, de la "caja", sale un resultado, un "producto".
Qu� pasa dentro de esa "caja negra" depende; si somos nosotros quienes hemos de programarla, lo sabremos, pero si no, no tenemos por qu�. Para poder usar la funci�n s�lo necesitaremos saber qu� datos de entrada admite, y de qu� tipo ser� el resultado. Hay que remarcar un detalle importante: las funciones devuelven un UNICO VALOR.
Por ejemplo; dentro de un programa, podemos querer calcular la media aritm�tica de una serie de datos. En principio, nosotros lo escribimos cuando tenemos que hacer los c�lculos. Pero ahora, resulta que m�s adelante tenemos que volver a calcular la media aritm�tica de otros datos. Y m�s adelante, otra vez. �Vamos a escribir el c�digo tantas veces? �No ser�a m�s l�gico definirnos una funci�n que se encargara de esa parte, y llamarla cuando la necesitemos?
Muy bien... �y c�mo definimos una funci�n? Pues de la siguiente manera:
funcion NOMBRE (arg1,...,argN) : TIPO
variables
......... {se declaran}
accion1
.......
accionN
Resultado <- Valor
fin funcion
TIPO es el tipo de dato que devolver� la funci�n al terminar de hacer su trabajo. NOMBRE es el nombre que le vamos a dar a la funci�n; por ejemplo, nuestra funci�n se puede llamar Pepe o se puede llamar Media_Aritmetica. arg1 ... argN es la lista de par�metros que vamos a pasar a la funci�n. La secci�n "variables" es una secci�n donde se declarar�n las variables a usar por la funci�n. M�s adelante hablar� del �mbito de las variables, para que se entienda el por qu� de esto.
accion1 ... accionN es toda la faena que debe hacer la funcion. Al final de esa faena, la funci�n devuelve un Resultado, que es el que hemos especificado como "Valor". �Y a d�nde va a parar ese "Valor"? Bueno, es que para poder usar una funci�n, tenemos que *invocarla*, llamarla de alguna manera. Si las funciones son cajas que devuelven valores, tendremos que disponer alg�n sitio para meter ese valor que nos devuelva la funci�n.
�C�mo la llamamos?
Para poder llamar a una funci�n, tendremos que tener definida en nuestra declaraci�n de variables una variable del MISMO tipo que devuelva la funci�n. Entonces, lo que hacemos es asignar a esa variable lo que nos devuelva la funci�n, haciendo lo siguiente:
Variable <- Nombre_Funcion(arg1, ..., argN)
Esta l�nea hace lo siguiente: llama a la funci�n Nombre_Funcion, pas�ndole los par�metros arg1, ..., argN; entonces, se ejecuta el c�digo de la funci�n, hasta que llega al final, momento en que devuelve un valor, y este valor devuelto es asignado a la variable Variable.
Vamos a ver un ejemplo. Supongamos que queremos hacer un programa que calcule, en varios puntos, la suma de los N primeros n�meros naturales, pero este N var�a conforme el programa lo necesita. Queremos hacer una funci�n que nos simplifique el trabajo. �C�mo lo hacemos? Bueno, lo primero que hay que plantearse siempre es qu� par�metros necesita la funci�n para trabajar, qu� tipo de valor va a devolver y, por �ltimo, c�mo va a hacer lo que tenga que hacer la funci�n.
En nuestro caso, la funci�n s�lo necesita saber qui�n es N, que ser� de tipo entero; como la suma de naturales es natural, el resultado a devolver tambi�n tendr� que ser una variable de tipo entero. Falta ver c�mo implementamos esa funci�n. Por ejemplo, lo podemos hacer as� (no voy a entrar ahora en mejoras):
funcion Suma_N_Naturales(ENTERO N) : ENTERO
variables
ENTERO: Suma,i
Suma <- 0
desde i<-1 hasta i=N hacer
Suma <- Suma+i
Resultado <- Suma
fin funcion
y ahora, vamos a usarla. En nuestro programa podemos poner:
Declaracion variables
ENTEROS: N, Suma
fin declaracion variables
inicio
desde N=1 hasta N=200 hacer
Suma <- Suma_N_Naturales(N);
mostrar por pantalla ('La suma de los ',N,' primeros naturales es ',Suma)
fin desde
fin
Con esto, hacemos 200 veces, incrementando en 1 cada vez N, la asignaci�n a la variable Suma del resultado obtenido por la funci�n Suma_N_Naturales, y mostrando por pantalla el resultado. Cada vez que se llegue a la l�nea de la asignaci�n, se llamar� a la funci�n Suma_N_Naturales, se ejecutar� el c�digo de esa funci�n, y al devolver el resultado, el programa principal recupera el control de la ejecuci�n.
Sin embargo, dentro de la funci�n tenemos declarada una variable que se llama Suma, y en el programa principal hay otra variable que se llama Suma... �c�mo sabemos cu�l es la buena? �no se mezclan ni nada parecido los valores?
Bueno, creo que este es un buen momento para hablar de...
 ��mbito de las variables
��mbito de las variables
Como ya hemos visto, un programa no tiene por qu� estar formado por un �nico m�dulo (vamos a llamarle as�) principal, si no que puede estar formado por muchas funciones, y por muchos procedimientos (de los que hablaremos m�s adelante). Cada funci�n, o cada procedimiento, puede tener, dentro de su secci�n de declaraci�n de variables, sus propias variables, aunque se llamen igual que las de la funci�n de m�s arriba, puesto que, al declarar una funci�n o un procedimiento, las variables que usan son LOCALES a ellos, es decir, s�lo ellos saben que existen y, por tanto, pueden usarlas.
Como contraposici�n a las variables locales, tenemos las GLOBALES, que se declaran en una secci�n VARIABLES GLOBALES; estas variables son reconocidas por cualquier funci�n o procedimiento que exista en nuestro programa, cualquiera puede modificar su valor en cualquier momento.
Ahora, �y si hay una variable global que tiene el mismo nombre que una variable local en una funci�n que estoy usando? En ese caso, se usa la variable que es local a la funci�n.
En nuestro ejemplo no se da este conflicto, al no haber una secci�n de variables globales (eso implica que no las hay), ya que cada variable Suma pertenece a una funci�n distinta.
Algunas notas respecto al tema de funciones:
Es una buena costumbre escribir, justo antes de la definici�n de la funci�n, un comentario sobre qu� hace la funci�n, para qu� nos van a servir los par�metros que vamos a pasarle, y qu� es lo que devuelve.
Hay que distinguir entre lo que se llama par�metros FORMALES y par�metros ACTUALES.
Cuando definimos una funci�n, en su CABECERA (la l�nea donde pone su nombre, los argumentos que recibe y el tipo de valor que devuelve) aparecen nombrados los argumentos. El nombre que ponemos en ese momento es lo que se llama par�metros formales. Pero, cuando la llamamos, por ejemplo, Suma_N_Naturales(27), le estamos pasando el par�metro concreto 27: a estos par�metros se les llama par�metros actuales.
Como ejercicio, escribid una funci�n que devuelva el resultado de:
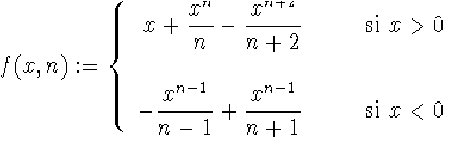
siendo x un n�mero real y n un n�mero natural.
 �Procedimientos
�Procedimientos
Se llama as� a un subprograma que ejecuta unas ciertas acciones sin que valor alguno de retorno est� asociado a su nombre. En otras palabras: NO devuelven valores (en cierto sentido).
Los procedimientos son normalmente llamados desde el algoritmo principal mediante su nombre y una lista de par�metros actuales (como las funciones) a trav�s de una instrucci�n espec�fica:
LLAMAR (CALL, en ingl�s)
Se diferencian de las funciones en que los par�metros de llamada pueden ser modificados si as� se especifica dentro del procedimiento; en ese sentido se puede interpretar como que devuelven valores.
La forma de declararlos es la siguiente:
PROCEDIMIENTO Nombre (Lista de par�metros formales) variables acci�n1 ....... acci�nN Fin Procedimiento
y la forma de usarlos:
LLAMAR_A Nombre(Lista de par�metros actuales)
Vamos a ver un ejemplo de todo esto: queremos tener una forma de calcular la suma, la resta, el producto y el cociente de dos n�meros cualesquiera. Obviamente, vamos a necesitar 6 variables; 2 de ellas ser�n los factores, y las otras 4, el resultado de las correspondientes operaciones. Podr�amos pensar en 4 funciones que devolvieran cada una de ellas un n�mero (entero, real, ...), pero podemos hacer esto de forma m�s compacta con un procedimiento. Veamos c�mo lo declarar�amos:
PROCEDIMIENTO Cuentas(ENTERO a, ENTERO b, ENTERO sum, ENTERO dif,
ENTERO mul, ENTERO dif)
sum <- a+b
dif <- a-b
mul <- a*b
div <- a/b
Fin Procedimiento
y luego lo podr�amos llamar as�:
LLAMAR_A Cuentas(5, 3, SUMA, RESTA, MULT, DIV)
con lo que a las variables SUMA, RESTA, MULT, DIV les ser�an asignados sus correspondientes valores; estas variables se supone que ya est�n declaradas previamente.
Y llegamos al �ltimo punto de esta entrega:
 �Recursividad
�Recursividad
Una buena definici�n de este concepto es la siguiente.
Recursivo: ver recursivo
... :-D ... O:-)
Aunque, si lo quereis de otra forma: propiedad de una funci�n o de un subprograma de llamarse a s� mismo.
Ilustremos esto con un ejemplo, nuestra funci�n para sumar los N primeros n�meros naturales. Vamos a escribirla de esta otra forma:
funcion Suma_N_Naturales(ENTERO N) : ENTERO
variables
ENTERO: Suma
si (N=1) entonces
Suma <- 1
si no
Suma <- N+Suma_N_Naturales(N-1)
fin si
Resultado <- Suma
fin funcion
Y vamos a llamarla con Suma_N_Naturales(4), detallando los pasos:
si (4=1) {falso, no se ejecuta}
si no {cierto, se ejecuta}
Suma <- 4+Suma_N_Naturales(4-1) {4-1=3}
Entramos en Suma_N_Naturales(3):
si (3=1) {falso, no se ejecuta}
si no {cierto, se ejecuta}
Suma <- 3+Suma_N_Naturales(3-1) {3-1=2}
Entramos en Suma_N_Naturales(2):
si (2=1) {falso, no se ejecuta}
si no {cierto, se ejecuta}
Suma <- 2+Suma_N_Naturales(2-1) {2-1=1}
Entramos en Suma_N_Naturales(1):
si (1=1) entonces Suma <- 1
y se devuelve el control al punto donde se llam� a Suma_N_Naturales(2), donde tenemos Suma <- 2+1, con lo que se devuelve el control al punto donde se llam� a Suma_N_Naturales(3), teniendo Suma<-3+(2+1), momento en el que se devuelve el control al punto donde se llam� a Suma_N_Naturales(4), donde tenemos Suma <- 4+(3+(2+1)), justo el resultado esperado.